trieungoinhaxanh
trieungoinhaxanh
Trang chủ Uncategorized Tứ diện đều - Thể tích tứ diện đều

Tứ diện đều - Thể tích tứ diện đều

Để vấn đáp mang đến thắc mắc Tứ diện đều là gì? Tính hóa học và phương pháp tính thể tích tứ diện đều như vậy nào?, ..... GiaiToan.com xin xỏ ra mắt cho tới quý thầy cô và chúng ta học viên tư liệu Thể tích tứ diện. Tài liệu canh ty chúng ta học viên ôn luyện và gia tăng kiến thức và kỹ năng Toán 12 cùng theo với này đó là cơ hội vận dụng công thức nhằm thực hiện những dạng bài xích tâp trắc nghiệm Toán lớp 12 tương đương ôn thi đua trung học phổ thông Quốc Gia. Mời thầy cô và chúng ta học viên nằm trong xem thêm tư liệu.

1. Tứ diện đều

Trước khi tìm hiểu hiểu tứ diện đều, tao nên nắm chắc thế này là hình tứ diện?

Bạn đang xem: Tứ diện đều - Thể tích tứ diện đều

- Tứ diện là hình với tứ đỉnh, thông thường được kí hiệu A, B, C, D. Bất kì điểm này nhập số những điểm bên trên được gọi là đỉnh, mặt mày tam giác đối lập với đỉnh này được gọi là lòng.

- Ví dụ: Cho tứ diện ABCD nếu lọc B là đỉnh thì (ACD) là mặt mày lòng.

Tứ diện đều

Tứ diện đều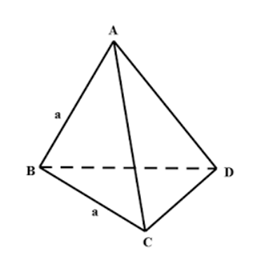Tứ diện đều là tứ diện với 4 mặt mày là tam giác đều.

Tứ diện đều là 1 hình chóp tam giác đều.

Hình chóp tam giác đều phải sở hữu tăng ĐK cạnh mặt mày bởi vì cạnh lòng là tứ diện đều.

2. Tính hóa học tứ diện đều

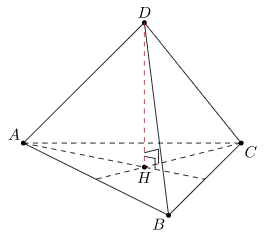
- Cho tứ diện đều ABCD như hình vẽ. Tứ diện đều phải sở hữu Điểm sáng như sau:

Tứ diện đều

\left\{ {\begin{array}{*{20}{c}} {AB = BC = CD = AD = DC = DB} \\ {{S_{ABC}} = {S_{ABD}} = {S_{BCD}} = {S_{ADC}}} \end{array}} \right.

- Tứ diện đều phải sở hữu những đặc điểm như sau:

+ Bốn mặt mày xung xung quanh là những tam giác đều cân nhau.

+ Các mặt mày của tứ diện là những tam giác với phụ vương góc đều nhọn.

+ Tổng những góc bên trên một đỉnh bất kì của tứ diện là 1800.

+ Hai cặp cạnh đối lập nhập một tứ diện có tính nhiều năm cân nhau.

+ Tất cả những mặt mày của tứ diện đều tương tự nhau.

+ Bốn đàng cao của tứ diện đều phải sở hữu phỏng nhiều năm cân nhau.

+ Tâm của những mặt mày cầu nội tiếp và nước ngoài tiếp nhau, trùng với tâm của tứ diện.

+ Hình vỏ hộp nước ngoài tiếp tứ diện là hình vỏ hộp chữ nhật.

+ Các góc bằng phẳng nhị diện ứng với từng cặp cạnh đối lập của tứ diện cân nhau.

+ Đoạn trực tiếp nối trung điểm của những cạnh đối lập là 1 đường thẳng liền mạch đứng vuông góc của tất cả nhì cạnh bại liệt.

+ Một tứ diện với phụ vương trục đối xứng.

+ Tổng những cos của những góc bằng phẳng nhị diện chứa chấp và một mặt mày của tứ diện bởi vì 1.

3. Thể tích tứ diện đều

a. Thể tích tứ diện ABCD: Thể tích của một khối tứ diện bởi vì 1 phần phụ vương tích số của diện tích S mặt mày lòng và độ cao của khối tứ diện tương ứng:

b. Thể tích khối tứ diện vuông

Giả sử mang đến tứ diện OABC với OA, OB, OC song một vuông góc tao được một khối tứ diện vuông. Thể tích của chính nó là:

Xem thêm: "Cận Thị" trong Tiếng Anh là gì: Định Nghĩa, Ví Dụ Anh Việt

4. Công thức tính nhanh chóng thể tích tứ diện đều cạnh a

Cho tứ diện đều SABC cạnh a. SG là đàng cao của hình chóp S.ABC, G nằm trong (ABC) thì G được xem là tâm của tam giác đều ABC. Suy ra:

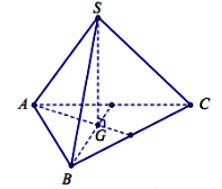Tứ diện đều

Chiều cao của hình chóp A.BCD đều cạnh a là: SG = h = \frac{{a\sqrt 6 }}{3}

Thể tích khối tứ diện đều cạnh a là: V = \frac{{{a^3}\sqrt 2 }}{{12}}

5. Bài thói quen thể tích khối tứ diện đều

Câu 1: Số mặt mày bằng phẳng đối xứng của hình tứ diện đều là:

A. 4 mặt mày phẳng

B. 6 mặt mày phẳng

C. 8 mặt mày phẳng

D. 10 mặt mày phẳng

Câu 2: Khối chóp tứ diện đều cạnh a rất có thể tích bằng:

A. 4 mặt mày phẳng

B. 6 mặt mày phẳng

C. 8 mặt mày phẳng

D. 10 mặt mày phẳng

Câu 3: Trung điểm những cạnh của một tứ diện đều tạo nên thành:

A. Các đỉnh của một hình nhì mươi mặt mày đều.

B. Các đỉnh của một hình mươi nhì mặt mày đều.

C. Các đỉnh của một hình chén bát diện đều.

D. Các đỉnh của một hình tứ diện.

Câu 4: Cho hình chóp tam giác đều S.ABC với cạnh lòng bởi vì a\sqrt 3, cạnh mặt mày tạo nên với lòng một góc 300. Tính thể tích khối chóp S.ABC theo đuổi a.

Câu 5: Cho tứ diện đều cạnh a\sqrt 3. Tính thể tích khối tứ diện a.

Câu 6: Cho hình chóp tam giác đều S.ABC với cạnh lòng bởi vì 4a, mặt mày mặt tạo nên với lòng một góc 450. Tính thể tích khối chóp S.ABC theo đuổi a.

Câu 7: Cho tứ diện ABCD với những cạnh AB, AC, AD song một vuông góc cùng nhau, AB = 3a, AC = 4a, AD = 5a. Gọi M, N, Phường theo lần lượt là trung điểm của những cạnh BC, CD, DB. Tính thể tích V của tứ diện AMNP theo đuổi a

Câu 8: Cho tứ diện ABCD với AC = 2a\sqrt 2, AB = CD = DA = DB = BC = 2a. Tính thể tích của tứ diện ABCD.

Câu 9: Cho tứ diện đều rất có thể tích V = \frac{{9{a^3}\sqrt 2 }}{4}. Tính phỏng nhiều năm những cạnh của tứ diện bại liệt.

Xem thêm: c%C3%A1i%20b%E1%BA%A3ng trong Tiếng Anh, dịch

------------------------------------------------------

Hy vọng tư liệu Bài luyện thể tích tứ diện đều sẽ canh ty chúng ta xúc tiếp với nhiều hình thức bài xích về phương trình lượng giác Toán 10, Toán 12. Chúc chúng ta ôn luyện thiệt tốt!

Một số tư liệu liên quan:

  • Tìm m nhằm hàm số nghịch ngợm đổi mới bên trên khoảng
  • Tìm m nhằm hàm số nghịch ngợm đổi mới bên trên R
  • Một vỏ hộp chứa chấp 5 ngược cầu đỏ hỏn không giống nhau và 3 ngược cầu xanh lơ không giống nhau với từng nào cơ hội lựa chọn ra 2 ngược nằm trong màu?
  • Cho những chữ số 0; 1; 2; 4; 5; 6; 8. Hỏi kể từ những chữ số bên trên lập được toàn bộ từng nào số với 5 chữ số không giống nhau...
  • Có từng nào số đương nhiên bao gồm 6 chữ số không giống nhau nhập bại liệt với đích thị 3 chữ số lẻ và 3 chữ số chẵn?
  • Một nhiều giác đều phải sở hữu số đàng chéo cánh gấp hai số cạnh. Hỏi nhiều giác bại liệt với từng nào cạnh?
  • Từ những số của tụ tập A = {0; 1; 2; 3; 4; 5; 6} rất có thể lập được từng nào số chẵn với 5 chữ số song một không giống nhau nhập bại liệt với nhì chữ số lẻ và 2 chữ số lẻ đứng cạnh nhau?
  • Một group học viên bao gồm 15 nam giới và 5 phái đẹp. Người tao mong muốn lựa chọn kể từ group rời khỏi 5 người nhằm lập trở thành một đội nhóm cờ đỏ
  • Một nhiều giác đều phải sở hữu số đàng chéo cánh gấp hai số cạnh. Hỏi nhiều giác bại liệt với từng nào cạnh?
  • Một người dân có 7 cái áo sơ-mi, nhập bại liệt với 3 cái áo sơ-mi trắng; với 5 cà vạt nhập bại liệt với 2 cà vạt gold color. Hỏi người bại liệt với từng nào cơ hội chọn 1 cái áo và một cà vạt vừa lòng điều kiện: nếu lọc áo White thì ko lựa chọn cà vạt color vàng
  • Tìm luyện xác lập của hàm con số giác
  • Xác toan x nhằm phụ vương số 1–x; x^2; 1+x theo đuổi trật tự lập trở thành một cấp cho số cộng?
  • Xếp tình cờ 6 học viên nam giới và 2 học viên phái đẹp trở thành một sản phẩm ngang
  • Từ những chữ số 1, 2, 3, 4 rất có thể lập được từng nào số đương nhiên bao gồm nhì chữ số không giống nhau?
  • Có từng nào số đương nhiên bao gồm 6 chữ số không giống nhau nhập bại liệt với đích thị 3 chữ số lẻ và 3 chữ số chẵn?
  • Phương trình lượng giác cơ bản
  • Một người dân có 7 cái áo sơ-mi, nhập bại liệt với 3 cái áo sơ-mi trắng; với 5 cà vạt nhập bại liệt với 2 cà vạt color vàng
  • Từ những chữ số 1, 2, 3, 4, 5, 6 rất có thể lập được từng nào số đương nhiên lẻ với 6 chữ số song một không giống nhau
  • Một group học viên bao gồm 15 nam giới và 5 phái đẹp. Người tao mong muốn lựa chọn kể từ group rời khỏi 5 người nhằm lập trở thành một đội nhóm cờ đỏ
  • Từ những chữ số 1, 2, 3, 4 rất có thể lập được từng nào số đương nhiên bao gồm nhì chữ số không giống nhau?
  • Một vỏ hộp chứa chấp 5 ngược cầu đỏ hỏn không giống nhau và 3 ngược cầu xanh lơ không giống nhau với từng nào cơ hội lựa chọn ra 2 ngược nằm trong màu?
  • Một group học viên bao gồm 15 nam giới và 5 phái đẹp. Người tao mong muốn lựa chọn kể từ group rời khỏi 5 người nhằm lập trở thành một đội nhóm cờ đỏ hỏn sao mang đến nên có một group trưởng nam giới, 1 group phó nam giới và với tối thiểu 1 phái đẹp. Hỏi với từng nào cơ hội lập group cờ đỏ hỏn.
  • Đội văn nghệ của một ngôi trường với 12 học viên, bao gồm 5 em học tập lớp A, 4 em học tập lớp B và 3 em học tập lớp C. Cần lựa chọn ra 4 em lên đường màn biểu diễn sao mang đến 4 chúng ta này nằm trong không thực sự 2 nhập 3 lớp bên trên. Hỏi với từng nào cơ hội lựa chọn như trên?

BÀI VIẾT NỔI BẬT